Question
Let denote the complement of an event Let be pairwise independent events with and Then equals (A) (B) (C) (D)
Found 7 tutors discussing this question
Discuss this question LIVE
7 mins ago
Filo tutor solution
Learn from their 1-to-1 discussion with Filo tutors.
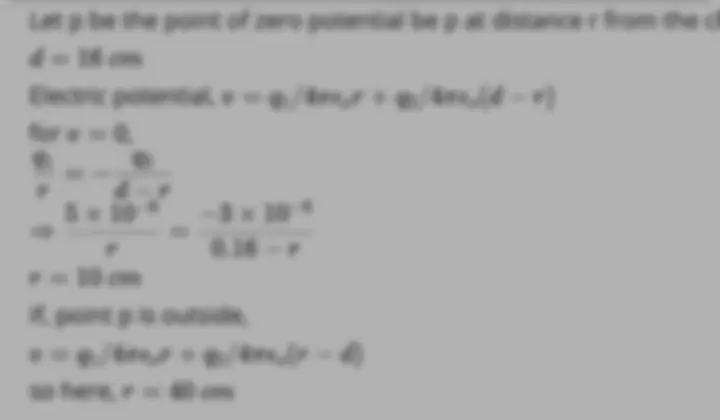
Generate FREE solution for this question from our expert tutors in next 60 seconds
Don't let anything interrupt your homework or exam prep with world’s only instant-tutoring, available 24x7

One destination to cover all your homework and assignment needs
Learn Practice Revision Succeed

Instant 1:1 help, 24x7
60, 000+ Expert tutors

Textbook solutions
Big idea maths, McGraw-Hill Education etc

Essay review
Get expert feedback on your essay

Schedule classes
High dosage tutoring from Dedicated 3 experts
Practice questions from similar books
Question 1
Cards marked with numbers 3, 4, 5, ......, 50 are placed in a box and mixedthoroughly. One card is drawn at random from the box. Find the probability thatnumber on the drawn card is dividing by 7.Question 2
One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will(i) be an ace.(ii) not be an ace.Question 3
Assume that each born child is equally likely to be a boy or a girl . If a family has two children, what is the conditional probability that both are girls given that(i) the youngest is a girl (ii) at least one is a girl?Question 4
Of the students in a school, it is known that 30% have 100% attendance and 70% students are irregular. Previous year results report that 70% of all students who have 100% attendance attain A grade and 10% irregular students attain A grade in their annual examination. At the end of the year, one student is chosen at random from the school and he was found to have an A grade. What is the probability that the student has 100% attendance ? Is regularity required only in school ? Justify your answer. 

Stuck on the question or explanation?
Connect with our maths tutors online and get step by step solution of this question.
231 students are taking LIVE classes
| Question Text | Let denote the complement of an event Let be pairwise independent events with and Then equals (A) (B) (C) (D) |



