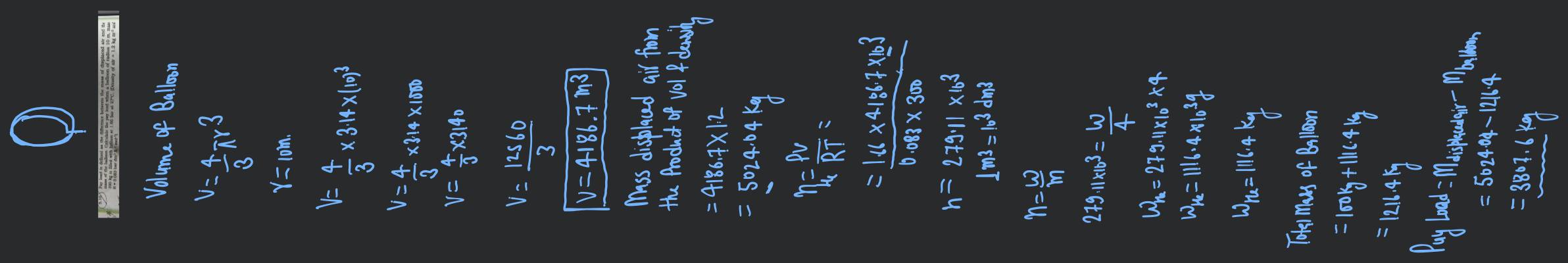Question
Hard
Solving time: 6 mins
Payload is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the payload, when a balloon of radius 10 m of mass 100 kg is filled with helium at 1.66 bar at 27 . (Density of air = 1.2 kg m and R = 0.083 bar dm K mol)
Found 4 tutors discussing this question
Discuss this question LIVE
15 mins ago
 Text solution
Text solution Verified
Verified
The volume of the balloon is .
The radius of balloon is 10 m.
Hence, the volume of the balloon is .
The mass of displaced air is obtained from the product of volume and density. It is .
The number of moles of gas present are .
Note: Here, the unit of volume is changed from to .
Mass of helium present is obtained by multiplying the number of moles with molar mass. It is kg.
The mass of filled balloon is the sum of the mass of the empty ballon and the mass of He. It is kg.
Pay load mass of displaced air mass of balloon kg
The radius of balloon is 10 m.
Hence, the volume of the balloon is .
The mass of displaced air is obtained from the product of volume and density. It is .
The number of moles of gas present are .
Note: Here, the unit of volume is changed from to .
.
Mass of helium present is obtained by multiplying the number of moles with molar mass. It is kg.
The mass of filled balloon is the sum of the mass of the empty ballon and the mass of He. It is kg.
Pay load mass of displaced air mass of balloon kg
Was this solution helpful?
38
Share
Report

One destination to cover all your homework and assignment needs
Learn Practice Revision Succeed

Instant 1:1 help, 24x7
60, 000+ Expert tutors

Textbook solutions
Big idea maths, McGraw-Hill Education etc

Essay review
Get expert feedback on your essay

Schedule classes
High dosage tutoring from Dedicated 3 experts
Practice more questions from Chemistry Part-I (NCERT)
Q1
Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm at 27 . (R = 0.083 bar dm K mol)
Q2
Payload is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the payload, when a balloon of radius 10 m of mass 100 kg is filled with helium at 1.66 bar at 27 . (Density of air = 1.2 kg m and R = 0.083 bar dm K mol)
Q3
Calculate the volume occupied by 8.8 g of CO at 31.1 and 1 bar pressure. (R = 0.083 bar L K mol)
View allPractice questions from Chemistry Part-I (NCERT)
Question 1
Easy
Views: 5,730
Question 2
Easy
Views: 5,567
Question 3
Medium
Views: 5,820
Question 4
Medium
Views: 6,060
Practice more questions from States of Matter
Question 1
Medium
Views: 5,578
Question 2
Easy
Views: 5,953
Practice questions on similar concepts asked by Filo students
Question 2
Views: 6,000
Question 3
Views: 5,539
Question 4
Views: 5,310


Stuck on the question or explanation?
Connect with our Chemistry tutors online and get step by step solution of this question.
231 students are taking LIVE classes
| Question Text | Payload is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the payload, when a balloon of radius 10 m of mass 100 kg is filled with helium at 1.66 bar at 27 . (Density of air = 1.2 kg m and R = 0.083 bar dm K mol) |
| Updated On | Jul 2, 2023 |
| Topic | States of Matter |
| Subject | Chemistry |
| Class | Class 11 |
| Answer Type | Text solution:1 Video solution: 1 |
| Upvotes | 149 |
| Avg. Video Duration | 12 min |