Question
In the reaction  the products are
the products are
Found 6 tutors discussing this question
Discuss this question LIVE
6 mins ago
Filo tutor solution
Learn from their 1-to-1 discussion with Filo tutors.
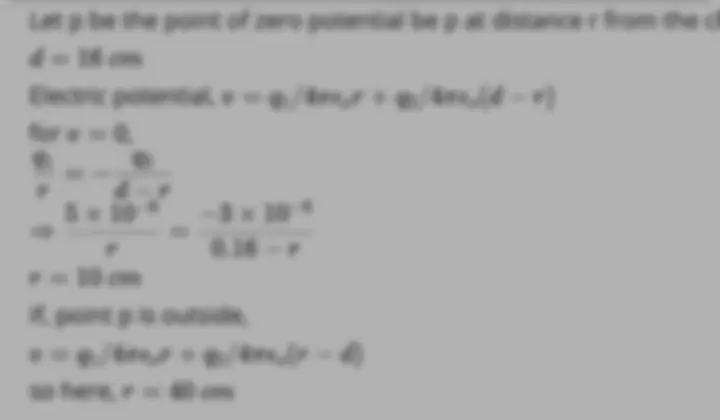
Generate FREE solution for this question from our expert tutors in next 60 seconds
Don't let anything interrupt your homework or exam prep with world’s only instant-tutoring, available 24x7

One destination to cover all your homework and assignment needs
Learn Practice Revision Succeed

Instant 1:1 help, 24x7
60, 000+ Expert tutors

Textbook solutions
Big idea maths, McGraw-Hill Education etc

Essay review
Get expert feedback on your essay

Schedule classes
High dosage tutoring from Dedicated 3 experts
Practice questions from similar books
Question 1
Perpendiculars are drawn from points on the line to the plane The feet of perpendiculars lie on the line (a) (b) (c) (d) 

Stuck on the question or explanation?
Connect with our all tutors online and get step by step solution of this question.
231 students are taking LIVE classes
| Question Text | In the reaction the products are |



