World's only instant tutoring platform
dropdown-logo
Become a tutorPartnershipsAbout usStudent loginTutor login
About us
Login
App StorePlay Store
Get 2 FREE Instant-Explanations on Filo with code FILOAPP
Consider a titration of potassium dichromate solution with aci
Question

Consider a titration of potassium dichromate solution with acidified Mohr's salt solution using diphenylamine as indicator. The number of moles of Mohr's salt required per mole of dichromate is

Views

Views: 780 students

tutor 0tutor 1tutor 2
Found 2 tutors discussing this question
Michael Discussed
Consider a titration of potassium dichromate solution with acidified Mohr's salt solution using diphenylamine as indicator. The number of moles of Mohr's salt required per mole of dichromate is
15 mins ago
Discuss this question LIVE
15 mins ago
Video Solution

Filo tutor solution

Learn from their 1-to-1 discussion with Filo tutors.

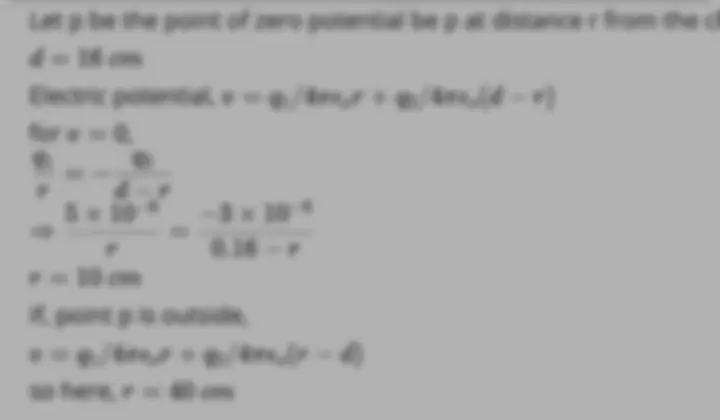
Solution Available
Generate FREE solution for this question from our expert tutors in next 60 seconds
Don't let anything interrupt your homework or exam prep with world’s only instant-tutoring, available 24x7

Practice questions from similar books

Question 1
The value of is ________.

View solution

Question 2
 Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length on y-axis is (are)

View solution

Question 3
Let P and Q be distinct points on the parabola such that a circle with PQ as diameter passes through the vertex O of the parabola. If P lies in the first quadrant and the area of the triangle is , then which of the following is (are) the coordinates of

View solution

Question 4
A pack contains cards numbered from 1 to . Two consecutive numbered cards are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller of het numbers on the removed cards is then ____________.

View solution

filo Logo
Question Text
Consider a titration of potassium dichromate solution with acidified Mohr's salt solution using diphenylamine as indicator. The number of moles of Mohr's salt required per mole of dichromate is