Question
Benzene and naphthalene form an ideal solution at room temperature. For this process, the true statement(s) is (are)
Found 2 tutors discussing this question
Discuss this question LIVE
15 mins ago
Filo tutor solution
Learn from their 1-to-1 discussion with Filo tutors.
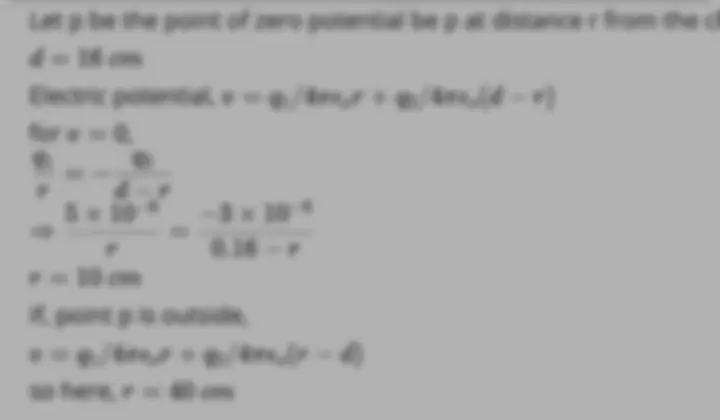
Generate FREE solution for this question from our expert tutors in next 60 seconds
Don't let anything interrupt your homework or exam prep with world’s only instant-tutoring, available 24x7
Practice questions from similar books
Question 1
·If the normals of the parabola drawn at the end points of its latus rectum are tangents to the circle , then the value of is Question 2
Let , be the number of red and black balls, respectively, in box I. Let ,be the number one red and b of red and black balls, respectively, in box II. One of the two boxes, box I and box II, was selected at random and a ball was drawn randomly out of this box. The ball was found to be red. If the probablity that this red ball was drawn from box II is then the correct option(s) with the possible values of , is(are) | Question Text | Benzene and naphthalene form an ideal solution at room temperature. For this process, the true statement(s) is (are) |



