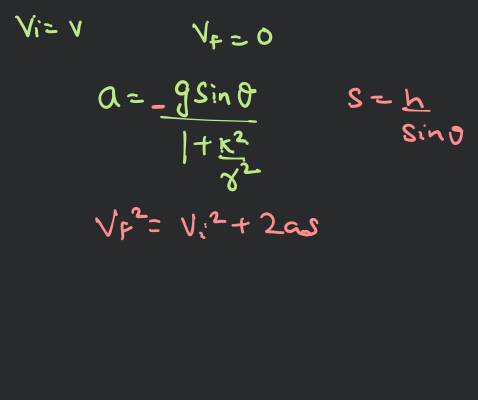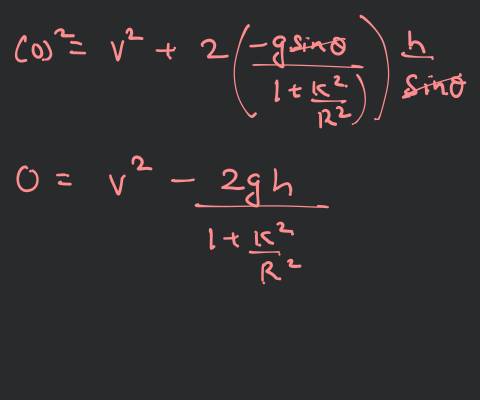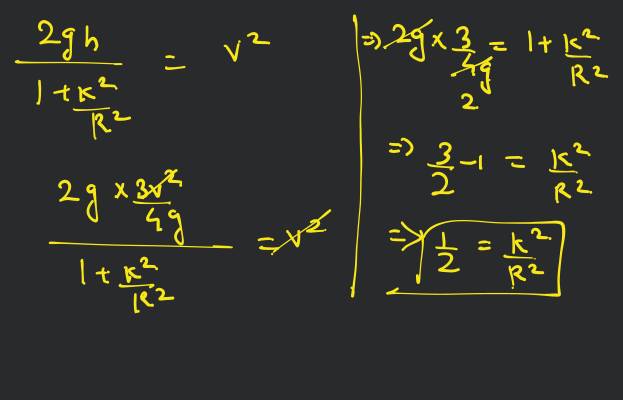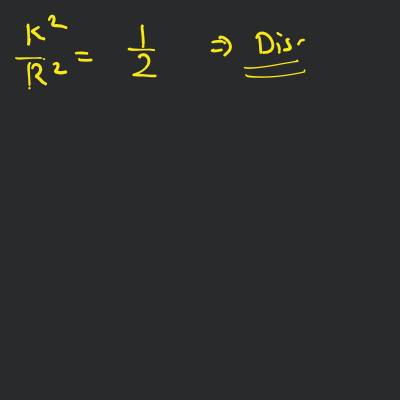Question
Medium
Solving time: 2 mins
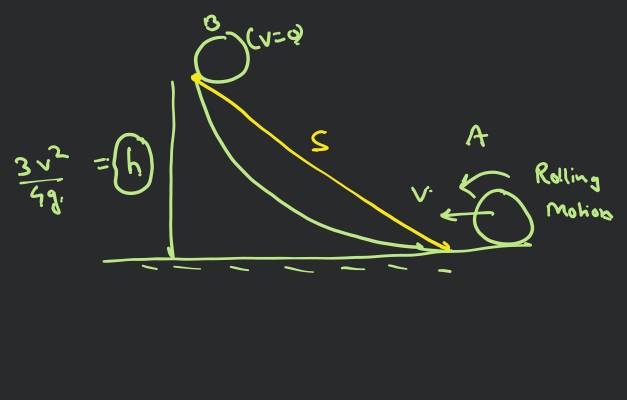
A small object of uniform density rolls up a curved surface with an initial velocity . It reaches upto a maximum height of with respect to the initial position. The object is :
Found 3 tutors discussing this question
Discuss this question LIVE
5 mins ago
 Text solution
Text solution Verified
Verified
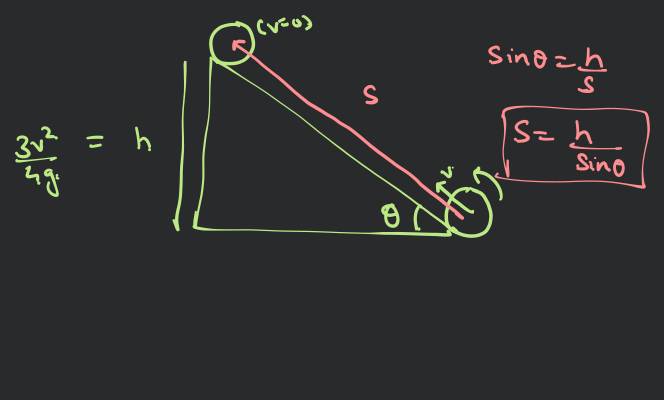
Using mechanical energy conservation
So, body is disc or solid cylinder.
So, body is disc or solid cylinder.
Was this solution helpful?
86
Share
Report
Filo tutor solutions (15)
Learn from their 1-to-1 discussion with Filo tutors.
3 mins
Uploaded on: 10/21/2022
Was this solution helpful?
70
Share
Report
6 mins
Uploaded on: 2/13/2024
Was this solution helpful?
58
Share
Report

One destination to cover all your homework and assignment needs
Learn Practice Revision Succeed

Instant 1:1 help, 24x7
60, 000+ Expert tutors

Textbook solutions
Big idea maths, McGraw-Hill Education etc

Essay review
Get expert feedback on your essay

Schedule classes
High dosage tutoring from Dedicated 3 experts
Questions from NEET 2013 - PYQs
Question 1
Easy
Views: 6,346
(g is the acceleration due to gravity)
Question 2
Easy
Views: 5,895
Question 3
Easy
Views: 5,763
Practice questions from Chemistry
Question 1
Easy
Views: 6,171
Question 2
Easy
Views: 6,629
Question 3
Easy
Views: 6,648
Practice questions from System of Particles and Rotational Motion in the same exam
Question 1
Easy
Views: 6,273
Question 2
Easy
Views: 6,181
Question 3
Easy
Views: 7,561
Practice more questions from System of Particles and Rotational Motion
Question 1
Medium
Views: 5,176
Question 2
Easy
Views: 5,686
Question 3
Medium
Views: 5,122
Practice questions on similar concepts asked by Filo students
Question 1
Views: 6,012
Question 2
Views: 5,811
Question 3
Views: 5,936


Stuck on the question or explanation?
Connect with our Physics tutors online and get step by step solution of this question.
231 students are taking LIVE classes
| Question Text | A small object of uniform density rolls up a curved surface with an initial velocity . It reaches upto a maximum height of with respect to the initial position. The object is : |
| Updated On | Feb 26, 2024 |
| Topic | System of Particles and Rotational Motion |
| Subject | Physics |
| Class | Class 11 |
| Answer Type | Text solution:1 Video solution: 15 |
| Upvotes | 1576 |
| Avg. Video Duration | 8 min |